Java完数实现教程：从概念到代码详解

在数学和编程的世界里，完数是一个既有趣又实用的概念。所谓完数，是指一个正整数等于它的所有真因子（即除了自身以外的约数）之和。比如6就是一个典型的完数，因为6的真因子是1、2、3，而1+2+3正好等于6。在Java编程中，实现完数的判断不仅能帮助我们理解数学概念，还能锻炼我们的编程思维和算法能力。

要判断一个数是否是完数，首先需要找出它的所有真因子，然后将这些因子相加，最后比较和是否等于原数。这个过程看似简单，但在实际编程实现中，需要考虑效率、边界条件等多个方面。下面我们就来详细探讨如何在Java中实现完数的判断。

Java完数判断的核心算法

完数的数学定义与特性

从数学角度看，完数有一些有趣的性质。首先，完数都是偶数（目前尚未发现奇完数），而且已知的完数都与梅森素数有关。在编程实现前，理解这些数学特性有助于我们优化算法。例如，我们可以利用完数都是偶数这一特性，在判断奇数时直接返回false，提高程序效率。

完数的另一个重要特性是它的稀缺性。虽然数学家们推测完数有无穷多个，但目前发现的完数却屈指可数。在编程实践中，这意味着我们可能需要处理大数的情况，这对算法的效率提出了更高要求。

Java实现完数判断的步骤详解

要在Java中实现完数判断，可以按照以下步骤进行：

编写一个方法接收一个整数参数
处理特殊情况（如输入小于等于1的数直接返回false）
找出该数的所有真因子
计算这些因子的和
比较和与原数是否相等

下面是一个基本的实现示例：

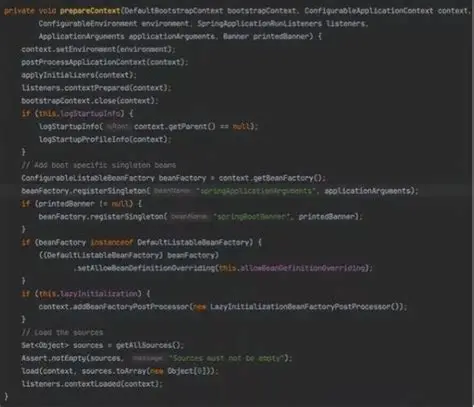
Java完数实现教程：从概念到代码详解

```java
public class PerfectNumber {
public static boolean isPerfectNumber(int num) {
if (num <= 1) {
return false;
}

    int sum = 1; // 1是所有大于1的数的真因子
    for (int i = 2; i * i <= num; i++) {
        if (num % i == 0) {
            sum += i;
            if (i != num / i) {
                sum += num / i;
            }
        }
    }

    return sum == num;
}

public static void main(String[] args) {
    System.out.println(isPerfectNumber(6));  // true
    System.out.println(isPerfectNumber(28)); // true
    System.out.println(isPerfectNumber(12)); // false
}

}


这段代码展示了2023年最新的完数Java实现方法，它通过遍历到√n来优化性能，避免了不必要的计算。对于每个找到的因子i，同时考虑其对应的因子num/i，这样可以减少循环次数。

## 完数判断中的常见问题与解决方案

在实际编程中，初学者可能会遇到几个典型问题。首先是边界条件处理不当，比如没有考虑输入为1或负数的情况。其次是算法效率问题，特别是当处理大数时，简单的遍历所有可能因子的方法会非常耗时。

另一个常见问题是因子重复计算。例如，在判断36时，6会被计算两次（作为2的对应因子和作为3的对应因子）。我们的示例代码通过条件判断`if (i != num / i)`避免了这个问题。

对于大数处理，可以考虑以下优化：
- 预先计算并存储已知完数（目前已知的完数并不多）
- 利用数学性质提前排除不可能的情况
- 使用更高效的因子查找算法

## 优化完数判断代码的实用技巧

要提高完数判断代码的效率，可以从以下几个方面入手：

1. **提前终止**：在因子求和过程中，如果和已经超过原数，可以立即返回false，无需继续计算。

2. **数学优化**：利用完数都是偶数这一特性，对奇数直接返回false（除非将来发现奇完数）。

3. **并行计算**：对于特别大的数，可以考虑将因子查找任务分配到多个线程并行处理。

4. **缓存结果**：如果需要多次判断相同的数，可以缓存已计算的结果。

下面是一个优化后的版本：

```java
public static boolean isPerfectNumberOptimized(int num) {
    if (num <= 1) return false;
    if (num % 2 != 0) return false; // 目前已知完数都是偶数

    int sum = 1;
    for (int i = 2; i * i <= num; i++) {
        if (num % i == 0) {
            sum += i;
            if (i != num / i) {
                sum += num / i;
            }
            if (sum > num) {
                return false; // 提前终止
            }
        }
    }
    return sum == num;
}

这段代码结合了多种优化技巧，是Java如何判断一个数是否是完数的高效实现。它特别适合需要频繁判断完数的场景。